西山yu

西山yu

日本語勉強中

Multiple Regression Analysis：Estimation

Chap4, Mar 10th, 2025

pdf version, html version

1. 一点提示：

  • 统计学：SSR（regression）SSE（error），计量经济学：SSE（explained）SSR（residual）
  • 自由度：
    • 伍： \(F=\frac{SSE/k}{SSR/(n-k-1)}\)
    • 张,南： \(F=\frac{RSS/k}{ESS/(n-k-1)}\)
    • 张,清： \(F=\frac{ESS/(k-1)}{RSS/(T-k)}\)
    • 伍： \(F=\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)}\)
    • 陈： \(F=\frac{(SSR^*-SSR)/m}{SSR/(n-K)}\)
  • SR与MR的比较（相同、不同与区别转化）：
\[R^2=\frac{SSE}{SST}=1-\frac{SSR}{SST}\] \[Var(\widehat{\beta}_1)_{mr}=Var(\widehat{\beta}_1)_{sr}\times VIF\]
  • 回归结果解读：
\[t=\frac{\widehat{\beta}_i}{se(\widehat{\beta}_i)}\] \[F=\frac{SSE/k}{SSR/(n-k-1)}=\frac{R^2/k}{1-R^2/(n-k-1)}\] \[F=\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)}=\frac{R_{ur}^2-R_r^2/q}{(1-R_{ur}^2)/(n-k-1)}\] \[\overline{R^2}=1-\frac{SSR/(n-k-1)}{SST/(n-1)}=1-(1-R^2)\frac{n-1}{n-k-1}\] \[SER=\widehat{\sigma}^2=\frac{\sum\widehat{u}_i^2}{n-k-1}\]

EViews结果解读： Stata结果解读：

2. 运用Venn图理解偏回归系数、遗漏变量、多重共线性

（整理自连享会gitee）

两步法：
第一步，用该解释变量对其他解释变量回归，得到OLS残差；
第二步，用y对第一步的残差回归。

三步法（与两步法等价）：

reg Y X1
predict u, res
reg X2 X1
predict e, res
reg u e

3. 遗漏变量偏误

\[y= \beta _0+ \beta _1x_1+ \beta _2x_2+ u\] \[\widetilde{y} = \widetilde{\beta } _0+ \widetilde{\beta } _1x_1\] \[x_2= \delta _0+ \delta _1x_1+ v\] \[\begin{aligned} y & =\beta_{0}+\beta_{1}x_{1}+\beta_{2}(\delta_{0}+\delta_{1}x_{1}+v)+u={(\beta_{0}+\beta_{2}\delta_{0})}+{(\beta_{1}+\beta_{2}\delta_{1})}x_{1}+{(\beta_{2}v+u)} \end{aligned}\]

偏误方向即 \(\beta_{2}\delta_{1}\) 的正负：

 \(Corr(x1, x2)>0\)\(Corr(x1, x2)<0\)
\(\beta_2>0\)\(+\)\(-\)
\(\beta_2<0\)\(-\)\(+\)

Wooldridge 6e, chap3:
(1)Example 3.4 Determinants of College GPA

corr colGPA hsGPA ACT
reg colGPA hsGPA ACT
reg colGPA ACT

(2)Example 3.6 Hourly Wage Equation
(3)Problem8

4. 多重共线性的识别与处理

当存在分组时，如果放入全部组别，Stata会自动删除一个组，以避免完全共线性问题。

识别方法：相关系数矩阵、方差膨胀因子（VIF）estat vif

处理方法：删除或重新定义变量、逐个放入

*如在auto.dta中，汽车长度和重量高度相关，可以定义长度和重量的复合变量：
gen wlr = weight/length

*又如伍德里奇第四章C11，使用两年学费的平均值比分别加入两者更好：
gen tuit = (tuit17 + tuit18)/2

5. （不要求掌握）高级估计方法：岭回归(Ridge Regression)

  • 大数据表现为“高维数据”，即特征向量的维度远大于样本容量。
  • 在传统实证研究中，样本量一般远大于变量个数：在上市公司的研究中，上市公司的数量大于回归中使用的特征变量个数——使用OLS没有问题

  • 但如果是某研究收集了100个病人的信息，其中每个病人均有2万条基因（即2万个特征变量），需要研究哪些基因导致了某种疾病。在这种高维数据的情况下，如果沿用OLS回归，就非常容易出现变量间的严重多重共线性问题。

  • OLS Regression: \(f=\sum_{i=1}^{n}(y_{i}-X\hat{\beta})^{2}\)
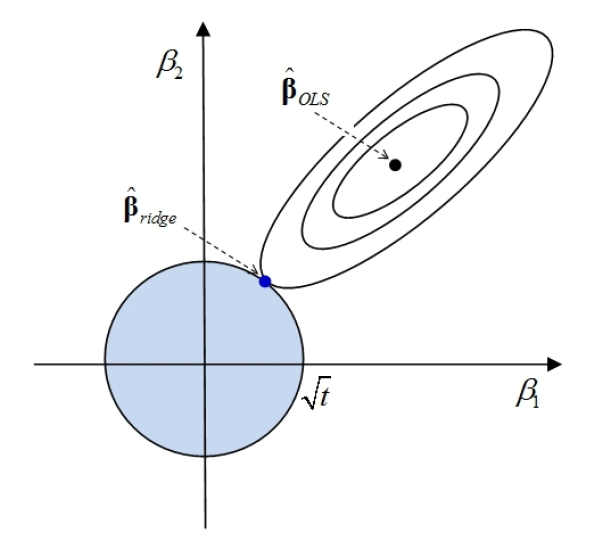
  • Ridge Regression: \(f=\sum_{i=1}^{n}(y_{i}-X\hat{\beta})^{2}+\lambda\sum_{j=1}^{p}\beta_{j}^{2}\)
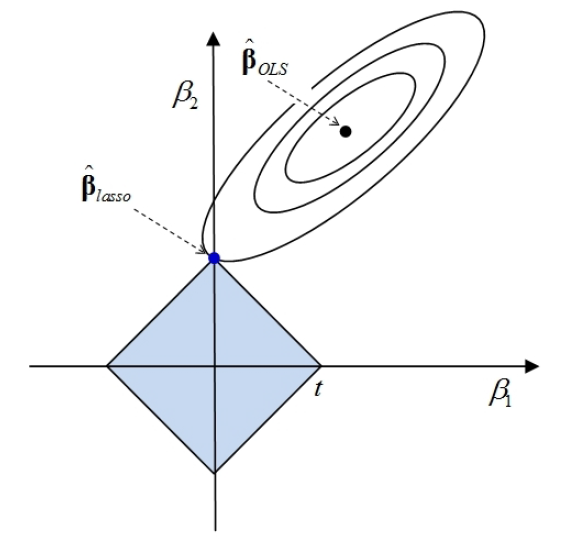
  • Lasso Regression: \(f=\sum_{i=1}^{n}(y_{i}-X\hat{\beta})^{2}+\lambda\sum_{j=1}^{p}|\beta_{j}|\)
   

Stata command:

  • Ridge Regression: ridgereg, rxridge
  • Lasso Regression: lassopack(lasso2, cvlasso, rlasso)
  • Elastic Net: elasticregress

参考资料：